
Important Notes:
- This is the 1st paper in which authors talked about “finding meaning in the latent variable”. If we change one dimention of a 100 dimentional vector, then we want to accociate meaning with that.
“Basicully, we want to find the mapping from latent vector to the generated images.”
And doing this will give us more control over the generated images.
“InfoGAN is a generative adversarial network that also maximizes the mutual information between a small subset of the latent variables and the observation. “
- to control the output of the InfoGAN we use two things,
- latent vectos $z$
- latent code $c$
So now, Generator is a function of $z$ and $c$, $G(z,c)$.
- Only when you are interpolating you will find meaning in $z$. By interpolation I mean the, arthmatic operation performed on averaged $z$ to change gender of a person waring glasses[man waring glasses -> woman waring glasses]. But when you want to associate meaning in $z$ there is no meaning its just a random vector.
- The latent vector[prior] $z$ is highly entangled and unstructured, it means we dont know what points in that vectors contatints the specific representation that we want. But we can introduce meaning in those $z$ vectors. To prove that Info-GAN comes to the picture.
- How introducing meaning in $z$ can help? By doing that you will make $z$ more interpretable. By that I mean, you will know how to adjust $z$ in order to get a desired output.
- So the paper, info-GAN is all about introducing meaning in the latent variables/codes (c1,c2..cn).

here you can see, that varying c1 in info-GAN will generate a consistent numbers in a row(same numbers in the row, although it has been sorted by the authors). But varying c1 in regular GAN will generate inconsistent results. In the image (c) you can see that varying $c_2$ in info-GAN targets the rotation of an digit, and in image (d) $c_3$ impacts the thickness/width of the digits. These properties of the dataset is called disentangled features/representations. For example:
Disentangled Representations,
- hair styles, presence/absence of eyeglasses and emotions on CelebA
- background digits from the central digit on SVHN
- pose from lighting of 3D rendered images
- writing styles from digit shapes on MNIST
- remember wheneven you read about disentanglment in the GAN literature, it is mainly has something to do with manipulation of the generated images by changing different properties of that image, eg: changing the width/rotation of the handwritten digits.
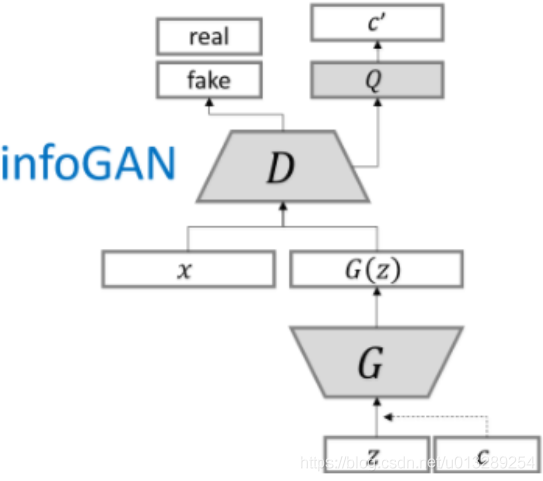
Info-GAN Framework:
- in info-GAN we provide two vectors [concatenated], 1) latent vector/prior, 2) latent code($c_1$,$c_2$ etc). Now the generator model $G$ is a function of $z$ and $c$, represented as $G(z,c)$.
- These latent codes are two types, discreate and continuous. From the above picture, $c_1$ is a categorical code.

- $c_2, c_3$ are continuous codes which continuous entangalments.

-
In the title we see information maximization GAN, but maximizing information b/t what? So, we try to maximize the information b/t $c$ and $G(z,c)$. Thats why we add the term $I(c;G(z,c))$in the objective function, $I$ is mutual information. The responsibility of modifying $c$ to increase the mutual info lies upon the $Q$ network. which is a part of discriminator network $D$, just with an aditional fully connected layer, this way it only adds a negligible computation cost to GAN.
-
By training infoGAN we get the Generator $G$ and the $Q$ network. the generator is used to generate new samples and the Q network is there to interpret the results. One example would be,
Assuming we have already trained an InfoGAN on the MNIST dataset, let’s say we want to generate a digit with a rotation angle of 45 degrees. We can do this by setting the c vector to [0, 0, 0.707, 0.707, 0], which corresponds to a rotation angle of 45 degrees in radians. We can also set the random noise vector z to a fixed value, such as [0.5, 0.5, 0.5, 0.5, 0.5].
Now, we can pass this generated image to the Q network to estimate the value of c that was used to generate it. The Q network will output a vector c’, which is an estimation of the true latent variable vector c.
In this case, the Q network might estimate a value of c’ = [0.01, -0.02, 0.71, 0.70, 0.02]. The third and fourth components of this vector (0.71 and 0.70) correspond to the sine and cosine of the rotation angle of 45 degrees, respectively.
-
You will find both representation of the info-GAN framework, but both are same, $Q$ uses $D$, just with a change of a extra fully connected layer.
| Q as a individual network | Q as a part of D |
|---|---|
 |
 |
Objective function:
Below is the objective function, separated in two parts, regular GAN loss + regularization [info-GAN loss].
$\min_{G} \max_{D} V_{I}(D, G)=V(D, G)- \lambda I(c ; G(z, c))$ , $\lambda < 0$ (mentioned in paper)
[GAN loss] $\min\limits_{G} \max\limits_{D} V(D,G) = E_{x \sim P_{data}(x)} [\log{D(x)}] + E_{z \sim P_{Z}(z)} [\log{(1 - D(G(z)))}]$
The 2nd part helps to increase the mutual information. Looking at the objective function you can tell that, training objective is to maximize the $D$ and minimize the $G$.
maximize $D$, $\max_{D} V_{I}(D, G) = \max_{D} E_{x \sim P_{data}(x)} [log(D(x))]$
and,
minimize $G$, $\min_{G} V_{I}(D, G)$ = $\min_{G} E_{z \sim P_{Z}(z)} [\log{(1 - D(G(z)))}] -\lambda I(c ; G(z, c))$ [coz these two terms includes generator part]
Here, to minimize the generator loss we need to increase $\lambda I(c ; G(z, c))$, on the other hand mutual information is defined as
$I(X ; Y)=H(X)-H(X \mid Y)=H(Y)-H(Y \mid X)$ …(a), Here $X = c$ and $Y = G(z,c)$
so to increase $\lambda I(c ; G(z, c))$ we need to minimize $H(X \mid Y)$. And when $H(X \mid Y) \to 0$ or $H(X \mid Y) = 0$, from information theory we say that, $X$ can be completely determined from $Y$. So now we can say, c can be completely determined from G(z,c). This is the base concept of info-GAN.
To optimize the mutual information $I$, we use the concept of Variational Mutual Information Maximization. which says, I is hard to maximize directly as it requires the access to the posterior $P(c|x)$, here $x$ implies $\hat{x}$. But we can get the lower bound of I, by defining an auxiliary distribution $Q(c|x)$.
By doing the calculations for $I$ by using equestion (a), you will eventually reach the position where, $I = H(c) + KLD(p,Q) +$ $E_{c \sim P(c), x \sim G(z, c)}[\log Q(c \mid x)]$ And as we know kld of two distribution is always $\geq 1$ , so using that we can write, $I \geq H(c) + E_{c \sim P(c), x \sim G(z, c)}[\log Q(c \mid x)]$. This is the lower bound.

From there we get,
$\min_{G, Q} \max_{D} V_{InfoGAN }(D, G, Q) = V(D, G) -\lambda L_{I}(G, Q)$
This is the main objective function of Info-GAN.
InfoGAN training process:
infoGAN is trained on 3 models D,G and Q. Q network is there to interprest the c latent variable for which we got a specific result. When training Q we try to increase the mutual information between $G(z,c)$ and $c$ which is $I(c; G(z,c))$ which is added as a regularization term to the original GAN loss function. it looks like this,
$\min_{G} \max_{D} V_{I}(D, G)=V(D, G)- \lambda I(c ; G(z, c))$ , $\lambda < 0$
We do the usual min-max game, the discriminarot tries to Maximize and the generator tries to minimize. But, what Q network does? Well if you simplify the above loss function, it turns out like this,
$\min {G, Q} \max _D V{\text {InfoGAN }}(D, G, Q)=V(D, G)-\lambda L_I(G, Q)$
$L_I(G, Q) \rightarrow \text { Variational Lower Bound }$
We minimize wrt G,
minimize $G$, $\min_{G} V_{I}(D, G, Q)$ = $\min_{G} E_{z \sim P_{Z}(z)} [\log{(1 - D(G(z)))}] -\lambda L_I(G, Q)$ [coz these two terms includes generator part]
We minimize wrt Q,
$minimize Q, V_I(D,G,Q) = \lambda L_I(G,Q)$
Questions that this Paper Answers:
NotImplementedErrorQuality Check:
NotImplementedErrorReferences:
NotImplementedError